ARBOLES BINARIOS
Un árbol binario es un grafo conexo, acíclico y no dirigido tal que el grado de cada vértice no es mayor a 3». De esta forma sólo existe un camino entre un par de nodos.
Un árbol binario con enraizado es como un grafo que tiene uno de sus vértices, llamado raíz, de grado no mayor a 2. Con la raíz escogida, cada vértice tendrá un único padre, y nunca más de dos hijos. Si reusamos el requerimiento de la conectividad, permitiendo múltiples componentes conectados en el grafo, llamaremos a esta última estructura un bosque.
 Tipos de árboles binarios
Tipos de árboles binarios
Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.
Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.
Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con cero hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura)
A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un árbol binario completo como un árbol binario lleno en el que todas las hojas están a profundidad n o n-1, para alguna n.
Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho.
ARBOL AVL
Arboles balanceados o equilibrados: · Un árbol binario de búsqueda es k-equilibrado si cada nodo lo es. · Un nodo es k-equilibrado si las alturas de sus subárboles izquierdo y derecho difieren en no más de k. Arboles AVL (Adel’son, Vel’skii, Landis) · Un árbol binario de búsqueda 1-equilibrado se llama árbol AVL. Cabe destacar que un árbol AVL no es un Tipo de dato abstracto sino una estructura de datos.
Árbol-B
B-árbol es un árbol de búsqueda que puede estar vacío o aquel cuyos nodos pueden tener varios hijos, existiendo una relación de orden entre ellos, tal como muestra el dibujo .
Un arbol-B de orden M (el máximo número de hijos que puede tener cada nodo) es un arbol que satisface las siguientes propiedades:
Cada nodo tiene como máximo M hijos.
Cada nodo (excepto raiz y hojas) tiene como mínimo M/2 hijos.
La raiz tiene al menos 2 hijos si no es un nodo hoja.
Todos los nodos hoja aparecen al mismo nivel,y no tienen hijos.
Un nodo no hoja con k hijos contiene k-1 elementos almacenados.
Los hijos que cuelgan de la raíz (r1, · · · rm) tienen que cumplir ciertas condiciones :
El primero tiene valor menor que r1.
El segundo tiene valor mayor que r1 y menor que r2 etc.
El último hijo tiene mayor que rm .
Un arbol B es un tipo de estructura de datos de árboles. Representa una colección de datos ordenados de manera que se permite una inserción y borrado eficientes de elementos. Es un índice, multinivel, dinámico, con un límite máximo y mínimo en el número de claves por nodo.

Crear el arbol B
Conserva las caracteristicas de los arboles binarios, AVL, y ABB.
Se busca la calve a insertar.
Si no esta en el arbol se comienza a insertar.
Si Esta llena la pagina:
Se divide la pagina en dos paginas al mismo nivel extrayendo la clave media
Con esta mediana se sube por el camino de busqueda.
Buscar
Clave = EB
Clave <= EB
Clave >= EB
ARBOL B+
Un árbol-B+ es una variación de un árbol-B. En un árbol-B+, en contraste respecto un árbol-B, toda la información se guarda en las hojas. Los nodos internos sólo contienen claves y punteros. Todas las hojas se encuentran en el mismo, más bajo nivel. Los nodos hoja se encuentran unidos entre sí como una lista enlazada para permitir búsqueda secuencial.
El número máximo de claves en un registro es llamado el orden del árbol-B+.
El mínimo número de claves por registro es la mitad del máximo número de claves. Por ejemplo, si el orden de un árbol-B+ es n, cada nodo (exceptuando la raíz) debe tener entre n/2 y n claves.
El número de claves que pueden ser indexadas usando un árbol-B+ está en función del orden del árbol y su altura.
Para un árbol-B+ de orden n, con una altura h:
Número máximo de claves es: nh
Número mínimo de claves es: 2(n / 2)h − 1
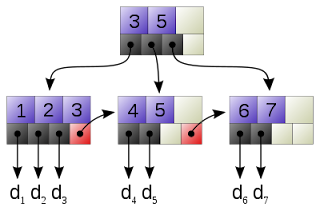
CARACTERISTICAS
Nodos internos solo contienen las claves o apuntadores.
Todas las hojas se encuentran al mismo nivel.
Nodos hojas se encuentran ligados como una lista enlazada para permitir la busqueda mas eficiente.
El minimo de claves es 2
OPERACIONES
Buscar
Insertar
Eliminar
PROGRAMA ARBOLES B+
public class BTree {
private BTree izquierda= null;
private BTree derecha= null;
private Object elemento;
public static int LADO_IZDO= 1;
public static int LADO_DRCHO= 2;
public BTree(Object elemento) {
this.elemento = elemento ;
}
public Object getElement() {
return elemento;
}
public BTree getIzquierda() {
return izquierda;
}
public BTree getDerecha() {
return derecha;
}
public void insertar(BTree tree, int lado) throws BTreeException {
if (lado==LADO_IZDO) {
if (izquierda==null) izquierda= tree;
else throw new BTreeException("Ya hay un ?rbol enlazado");
}
else if (lado==LADO_DRCHO) {
if (derecha==null) derecha= tree;
else throw new BTreeException("Ya hay un ?rbol enlazado");
}
else throw new BTreeException("Lado incorrecto");
}
public BTree extraer(int lado) throws BTreeException {
BTree subarbol;if (lado==LADO_IZDO) {
subarbol= izquierda;
izquierda= null;
}
else if (lado==LADO_DRCHO) {
subarbol= derecha;
derecha= null;
}
else
throw new BTreeException("Lado incorrecto");
return subarbol;
}
public void imprimePreOrden() {
System.out.println(elemento);
if (izquierda!=null) izquierda.imprimePreOrden();
if (derecha!=null) derecha.imprimePreOrden();
}
public void imprimePostOrden() {
if (izquierda!=null) izquierda.imprimePostOrden();if (derecha!=null) derecha.imprimePostOrden();System.out.println(elemento); } public void imprimeEnOrden() {if (izquierda!=null) izquierda.imprimeEnOrden();System.out.println(elemento);if (derecha!=null) derecha.imprimeEnOrden(); }}*****************public class BTreeException extends Exception { public BTreeException (String mensaje) {super(mensaje); }}******************public class Trabalenguas { public static void main(String args[]) {BTree trabalenguas, subarbol, temporal;try { trabalenguas= new BTree("Tres"); subarbol= new BTree("tristes"); trabalenguas.insertar(subarbol, BTree.LADO_IZDO); temporal= new BTree("tigres"); trabalenguas.insertar(temporal, BTree.LADO_DRCHO); temporal= new BTree("com?an"); subarbol.insertar(temporal, BTree.LADO_IZDO); temporal= new BTree("trigo"); subarbol.insertar(temporal, BTree.LADO_DRCHO);} catch (BTreeException ex) { System.out.println(ex.getMessage()); return;}trabalenguas.imprimePreOrden();System.out.println("------------------");trabalenguas.imprimeEnOrden();System.out.println("------------------");trabalenguas.imprimePostOrden();System.out.println("------------------");System.out.println("------------------");try { subarbol= trabalenguas.extraer(BTree.LADO_IZDO);} catch (BTreeException ex) { System.out.println(ex.getMessage()); return;}trabalenguas.imprimePreOrden(); }}











